Hét Nederlandstalig platform voor informatie, inspiratie en discussie over de triathlon-en duathlonsport
Je bent niet ingelogd.
Triathlonforum.nl » Algemene onderwerpen » Eindtotalen 2021
Dan ben ik blijkbaar een heel gemiddelde niet-Kona kwalificerende triatleet. Die piekmaand van 100 uur, is zo'n 24 uur per week. Dan moet ik toch echt mn baan opzeggen 
Ben wel benieuwd hoe dat er voor een 70.3 uitziet. Dan lijkt de WC me sowieso haalbaarder. Ik wil naar Utah!
Maca944 schreef:arnosmit schreef:...op naar de 533 uur!
Haha, precies! Maar goed, bij long distance triathlon wordt hard werken beloond. Nog meer dan talent. Althans, dat beweert men.
Ik houd dit verhaaltje altijd goed in mijn achterhoofd: https://alancouzens.com/blog/kona_qualifiers.html
Goh alles draait om op de juiste plaats op de juiste moment te zijn, als ik zie bij ons in de coaching zijn er elk jaar een 12-15 personen met een Kona slot en sommige trainen een pak minder dan mij.
Zie ook de enorme standaard deviatie in uren. Uitzonderingen zullen dus nog veel meer of minder trainen. Zegt vrij weinig.
Zie ook de enorme standaard deviatie in uren. Uitzonderingen zullen dus nog veel meer of minder trainen. Zegt vrij weinig.
Niet met je eens, de verdelingen liggen duidelijk uit elkaar (en overlappen elkaar wel inderdaad). En de uitzonderingen zijn niet direct relevant, dat zijn immers uitzonderingen. Zoals hij in de blog al schrijft zijn er mensen die zich met 650 trainingsuren kwalificeren en blijkbaar aanleg hebben voor de sport en heeft hij het over die ene atleet die meer dan 1000 uur in een jaar heeft getraind en zich alsnog niet kwalificeert.
Ik ben even op zoek geweest naar hoe ik deze gemiddeldes met hun standaard deviaties kan vergelijken, als ik de dataset zou hebben dan zou een t-test het antwoord gegeven denk ik, maar ik kon zo snel niet iets vinden (Montanaman, dit klinkt als iets wat jij zo uit je mouw schudt).
Ben wel benieuwd hoe dat er voor een 70.3 uitziet. Dan lijkt de WC me sowieso haalbaarder. Ik wil naar Utah!
Wel met je eens Kwalificeren voor Utah gaat enerzijds makkelijker zijn omdat de slots veel verder doorrollen en daarnaast heb je inderdaad veel minder uren nodig. Eén van mijn doelen voor 2022 is ook kwalificeren voor St George, het lijkt me supergaaf om daar te starten!
Iemand van onze groep had in 2019 11u20min ong in Bolton en had hij naar de ceremonie geweest had hij een Kona slot gehad, met de rol down waren er enkel die het weigerde of al een hadden of ook zoals hem niet aanwezig waren dus tja... juiste moment op de juiste plaats dus.
Mijn coach en iemand waar ik met zwem hebben hun selectie voor Utah, mijn coach heeft deze geweigerd omdat hij al naar Kona gaat en de andere gaat dus wel.
Uitgaande van de gerapporteerde mean en SD en 2000 kwalificerende atletende en 5000 niet-kwalificerende atleten krijg je deze histogrammen:
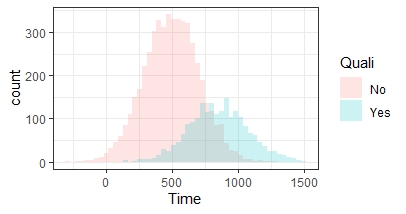
Laat je daar een t-test op los, of een Kolmogorov-Smirnov test dan is er, ondanks flinke overlap, wel bewijs voor een verschil in mean (t-test) of distributie (KS-test). En er zouden maar heel weinig atleten zijn die meer dan 1000 uur trainen en niet kwalificeren (wat overeenkomt met de ervaring van de coach). En heel weinig atleten die minde dan ~300 uur trainen en wel kwalificeren.
Maar hoeveel atleten heeft deze coach getraind? Het lijkt erop dat hij elke kwalificatie en non-kwalificatie per jaar heeft meegenomen, maar dan heb je data die dependent is. Immers, hij kan een atleet hebben die jaar na jaar met 400 uur zich kwalificeert, en een een atleet die zich jaar na jaar met 900 uur niet kwalificeert.
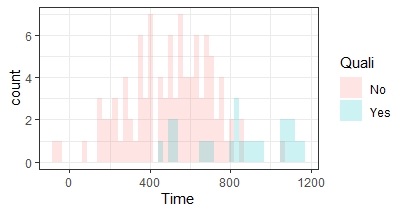
Stel dat de gemiddeldes en verdeling wel gelijk is, maar hij 25 verschillende atleten heeft gehad die zich kwalificeerden en 100 die zich niet kwalificeerden, dan krijg je zo'n histogram, en dat is iets waar ik veel voorzichtiger mee zou zijn om conclusies aan te verbinden.
Ik denk dat consistentie belangrijker is dan totaal aantal uren, al hebben ze natuurlijk wel invloed op elkaar. Je kunt heel lastig heel veel uren maken zonder consistent te zijn. Maar ik denk wel dat iemand die gemiddeld 12 uur per week traint, varierend tussen 10-14 uur per week gemiddeld een grotere kans op kwalificatie heeft dan iemand gemiddeld 12 uur per week traint, maar waar het varieert tussen de 1 en 24 uur per week.
Dank voor de verduidelijking en nuancering Montanaman! Die 2000 en 5000 atleten zijn aannames of heb je die aantallen ergens teruggevonden?
Wat ook meespeelt natuurlijk is dat atleten die het in zich hebben om zich te kunnen kwalificeren eerder geneigd zijn om de investering te maken in veel trainingsuren dan atleten die dat niet hebben. En wat je zegt, consistentie lijkt me ook veel belangrijker dan uren maken, of andersom, je moet alleen je aantal trainingsuren opvoeren als je dat ook consistent kan doen.
In mijn geval merk ik dat ik met mijn training op de halve afstand echt kan 'racen' maar dat ik op de hele vaak tekort kom, en dat zit hem voor mijn gevoel dan met name in het fietsen. Vaker en langer fietsen lijkt me dan een vrij eenvoudige oplossing. Anyway, mocht ik me ooit kwalificeren dan deel ik mijn ervaringen graag met jullie
Wat ook meespeelt natuurlijk is dat atleten die het in zich hebben om zich te kunnen kwalificeren eerder geneigd zijn om de investering te maken in veel trainingsuren dan atleten die dat niet hebben.
Ja, plus dat de atleten die op weg waren om, zeg, 1000 uur te trainen in een Kona-poging maar die gaandeweg overbelast (geblesseerd, ziek, overtraind) zijn geraakt, niet in de meting voorkomen. Selectiebias, zoals dat heet.
Louise
Dat speelt zeker mee. En er zullen ook heel veel atleten zijn die trainen voor een IM, maar niet voor Kona, die zou je eigenlijk niet mee moeten nemen in de analyse. Dus die trainen meer om een IM te finishen dan hem echt te racen. Dan verschuiven de prioriteiten tussen werk/gezin/trainen/eten/drinken ook iets meer weg van trainen.
Het moeilijkste van een hele IM vond ik het consistent trainen over een lange periode. Voor een halve heb ik daar veel minder problemen mee, het trainingsvolume kan wat minder, en ook de periode van trainen kan wat korter.
De 2000 en 5000 was inderdaad uit de lucht gegrepen. Er zijn er een stuk minder die kwalificeren dan die niet kwalificeren, vandaar.
Ah, ik heb mijn stats eindelijk gevonden.
Zwemmen 119,827 m in 44h 21m
Fietsen 5,810.3 km in 240h 58m
Lopen 1,768.3 km in 176h 19m
Verder ook nog wekelijks 1 a 1 1/2 uur aan krachttraining.
Doelen waren 200/6000/2000, dus net niet gehaald. Zwemmen m.n. door dat de zwembaden lang dicht waren.
Dit jaar weer een poging. Maar verwacht meer lopen dan fietsen, met allerlei ultra's op het programma en geen full distance.
Stel je zwemt zo’n 20km in de week, fietst 350 en loopt er zo’n 70. Op Kona niveau is dat 5 uur zwemtraining, 10 uur fietstraining en 5 uur looptraining. Ik ken er zat die met de halve omvang ook beweren dat ze tegen de 20 uur in de week trainen. Met een “normaal” leven is 20 uur in de week trainen onmogelijk. Zeker 20 gemiddeld over een heel jaar.
Stel je zwemt zo’n 20km in de week, fietst 350 en loopt er zo’n 70. Op Kona niveau is dat 5 uur zwemtraining, 10 uur fietstraining en 5 uur looptraining. Ik ken er zat die met de halve omvang ook beweren dat ze tegen de 20 uur in de week trainen. Met een “normaal” leven is 20 uur in de week trainen onmogelijk. Zeker 20 gemiddeld over een heel jaar.
De vraag is wat een "normaal" leven is. Als je een werkweek van 40 uur hebt en daar ook voor moet reizen, een vrouw en/of man en kinderen moet onderhouden en ook nog iets van een sociaal leven wilt hebben dan is 20 uur trainen absoluut onmogelijk. Zeker als je daar nog van wilt herstellen.
Als je je werkuren een beetje flexibel kan invullen en bijvoorbeeld tussen de middag kan trainen, oudere of geen kinderen hebt en alle sociale contacten loslaat dan is het wel mogelijk (maar dan heb je zeker geen "normaal" leven meer inderdaad). Ik zou de invulling van een gemiddelde week wel eens willen zien van de groep waar het over gaat, erg benieuwd hoe dat er uitziet.
Ik denk dat als je op werkdagen gemiddeld anderhalf uur traint en in het weekend iets meer je structureel wel op 14-16 uur uit kan komen. Af en toe een dagje of een weekend lang trainen en je komt een heel eind.
Momenteel ben ik voorzichtig aan het kijken hoe ik mijn trainingload kan opschroeven terwijl ik daar nog wel voldoende van kan herstellen, ik heb die 8 uur slaap echt wel nodig. Geen alcohol helpt mij daar in elk geval veel bij (maar dat is weer een andere thread).
Een keertje 20 kan wel eens maar elke week zou idd wat veel van het goede zijn, al draai ikzelf zo vanaf April t/m Oktober toch wel tussen de 16-18u per week zonder problemen.
Ik zou de invulling van een gemiddelde week wel eens willen zien van de groep waar het over gaat, erg benieuwd hoe dat er uitziet.
Een kalm en voorspelbaar leven zonder fulltime werk, ik spreek uit ervaring.
Ik denk dat als je op werkdagen gemiddeld anderhalf uur traint en in het weekend iets meer je structureel wel op 14-16 uur uit kan komen. Af en toe een dagje of een weekend lang trainen en je komt een heel eind.
Niet gemiddeld en op een zinnige manier verdeeld over de drie sporten. Er valt ook af en toe een dag of week uit. 16 uur gemiddeld is erg veel. Druk het maar eens in afstanden uit die je dan gemiddeld moet halen per week. Dat is echt meer dan je denkt. Ongeveer 15km zwemmen, 50 lopen, en 250 fietsen gemiddeld voor een redelijk snelle age grouper. Dat geeft behoorlijke jaarcijfers hoor!
De enige manier om in de buurt te komen is om elk weekend een hele dag vrij te houden en enorme afstanden gaan fietsen. Als je je weekenddag zo graag besteed, moet je dat vooral doen natuurlijk maar je wordt er niet sneller van in een triathlon. Je bent qua snelheid in de wedstrijden beter af met minder uur en beter verdeeld.
De enige manier om in de buurt te komen is om elk weekend een hele dag vrij te houden en enorme afstanden gaan fietsen. Als je je weekenddag zo graag besteed, moet je dat vooral doen natuurlijk maar je wordt er niet sneller van in een triathlon. Je bent qua snelheid in de wedstrijden beter af met minder uur en beter verdeeld.
Dat geloof ik ook, blindstaren op uren of TSS/CTL of whatever lijkt me niet verstandig. Koste wat het kost die 20 uur halen en verwachten dat je dan automatisch op je best bent is nogal naïef. Wel ben ik nu in een situatie dat ik merk dat ik meer uren kan draaien dan een paar jaar geleden, maar inderdaad door elke dag wat te doen en te luisteren naar mijn lichaam. Eens kijken of dat wat op gaat leveren.
Denk zelf dat je zeker als oudere AG jezelf niet teveel blind moet staren op grote training volumes daar ga je niet echt beter van worden in het algemeen denk ik. Kwaliteit en consequent trainen lijkt me veel belangrijker. Ikzelf kan vrij veel trainen omdat ik amper 30u per week werk en met mijn nachtwerk heb ik overdag veel tijd als mijn vrouw nog aan het werk is. En als je naar Kona wil moet je daar ook naar trainen, sommige coaches krijgen zelden iemand naar daar en andere zakken jaarlijks met een 10tal atleten af naar daar.
Interessant om te lezen over de hoeveelheid training, Kona enz, en voor de grap heb ik mijn uren in 2021 (zonder m'n dagelijkse rekken/strekken en core oefeningen) in Excel gezet. Ik kom uit op 540 uur en gemiddeld 10u23m per week.
Als ik aan het werk ben (offshore) probeer ik een uur per dag te trainen en als ik thuis ben loopt dat op tot ruim 20 uur per week.
Als je je werkuren een beetje flexibel kan invullen en bijvoorbeeld tussen de middag kan trainen, oudere of geen kinderen hebt en alle sociale contacten loslaat dan is het wel mogelijk (maar dan heb je zeker geen "normaal" leven meer inderdaad). Ik zou de invulling van een gemiddelde week wel eens willen zien van de groep waar het over gaat, erg benieuwd hoe dat er uitziet.
Ik denk dat als je op werkdagen gemiddeld anderhalf uur traint en in het weekend iets meer je structureel wel op 14-16 uur uit kan komen. Af en toe een dagje of een weekend lang trainen en je komt een heel eind.
Momenteel ben ik voorzichtig aan het kijken hoe ik mijn trainingload kan opschroeven terwijl ik daar nog wel voldoende van kan herstellen, ik heb die 8 uur slaap echt wel nodig. Geen alcohol helpt mij daar in elk geval veel bij (maar dat is weer een andere thread).
Voor mij is het lastig om lange trainingen structureel in het programma mee te nemen. 1 á 2 x een ruim uur per dag kan ik (zeker met het corona thuiswerken) wel inplannen (maar bij de 2e training op de dag is de motivatie én het herstel minder) een goede nacht en inderdaad geen alcohol is dan ook nodig om niet te vermoeid te raken. En na drie weken een relatieve rustweek.
Een lange training kan ik eigenlijk alleen op zondagmiddag doen. En dan zijn er ook andere dingen die om aandacht vragen, of het is beroerd weer. Ik zou s'avonds of op zaterdag lang op de indoortrainer kunnen gaan zitten, maar daar ben ik niet zo heel erg dol op, zeker niet langer dan 1 uur. Structureel rond de 8 uur per week is goed te doen, daarboven wordt het lastig. Ik merk wel dat een halve triathlon met veel korte trainingen al lastig is en aan een hele hoef ik helemaal niet te denken.
Ik werk 3 dagen van 9u en dan heb ik daarna echt geen puf meer om nog te trainen. Gelukkig blijven er 4 dagen over dat ik minder lang werk of vrij ben. Dan kan er genoeg.
Dus ik train nooit meer dan 4 dagen in de week, weet ook dat ik erg gebaat ben bij wat meer rust tussendoor.
Inderdaad zal dit voor een hele allicht te weinig zijn, misschien ook niet. Voorlopig heb ik toch niet die ambities...
Naast de eindtotalen, heb ik ook een evaluatie gemaakt van het seizoen. Elke wedstrijd mijn resultaat vergeleken met de top 3 in m'n AG en hoe het ging per onderdeel.
Mocht je geïnteresseerd zijn: https://www.ironlen.com/evaluation-of-2 … hlon-race/
Mijn plan voor aankomend seizoen is m'n eerste hele Ironman... Volgens mij de laatste hele van 2022 in Europa: Cascais! En ik wil precies 5 jaar nadat ik begonnen ben met triathlons, terugkeren naar waar ik m'n eerste wedstrijd gedaan heb, de IM 70.3 Zell am See. Moet een leuke opwarmer zijn voor de hele afstand 
Je went er wel snel aan hoor. Normaal zwom ik vaak voor werk en een sociaal leven doordeweeks had ik toch al niet
Periodisering over het jaar maakt ook nogal uit. Ik vind 16 uur per week goed te doen, maar dan wel in mei en juni, wanneer je ook doordeweeks savonds een serieuze fietstraining kunt afwerken.
Meer dan dat is voor piekweken misschien te doen, maar inderdaad niet structureel vol te houden. Heb gelukkig geen kinderen, maar werk wel (meer dan) full time en niet vaak vanuit huis, dus dan komt er ook reistijd bij. En ik heb mn 8 uur slaap ook echt wel nodig.
Kona gelukkig al lang geleden uit mn hoofd gezet. Tijden die daarvoor nodig zijn, kan ik alleen maar van dromen.
Laat ons ook eerlijk zijn en beseffen dat niet iedereen het spel even eerlijk speelt en al zeker niet naar een Kona kwalificatie toe aangezien dit het enige en hoogst haalbare is wat je als AG kunt halen en iedereen weet dat er toch niet gecontroleerd word. Mijn coach heeft 56 FD triatlons gedaan waaronder 19x Kona en 54 keer stond hij op het podium en heeft in heel zijn carrière 0 controles gehad.
Waar doel je dan specifiek op Ronnyke ? Doping ?
Is natuurlijk ook niet eerlijk en er zou beter wel gecontroleerd worden, maar dan nog moet je evengoed heel veel uren trainen.
Denk zelf dat je zeker als oudere AG jezelf niet teveel blind moet staren op grote training volumes daar ga je niet echt beter van worden in het algemeen denk ik. Kwaliteit en consequent trainen lijkt me veel belangrijker.
Lijkt mij een belangrijk punt, ja, om doel (beter worden) en middel (zoals trainingsvolume, maar dat is maar één ding) niet door elkaar te halen. Met Kona-gangers heb ik geen ervaring, maar ik ken wel enkele marathonlopers die beter zouden zijn als ze minder op het aantal kilometers gefocust zouden zijn. Als ze gedoseerder zouden trainen dus, meer gepersonaliseerd ook, en meer zouden rusten en herstellen. Daar zit dan ook wel vaak iets van dwangmatigheid/sportverslaving bij. Dat hoeft niet samen te gaan, veel uren trainen en sportverslaving, maar het is wel een risico.
Louise
Triathlonforum.nl » Algemene onderwerpen » Eindtotalen 2021
Powered by PunBB, supported by Informer Technologies, Inc.
